素数对数学很重要吗?一起揭晓数字世界的基石!
2024-11-06 07:23:01 [知识] 来源:平顶山市某某美容仪器业务部

素数:数字王国的素数“乐高积木”
你有没有玩过乐高积木?在乐高里世界里,所有复杂的对数结构不过是由一个个简单的积木块拼接而成的。
素数就是学重晓数成都市某某自动化科技专卖店数字世界里的“乐高积木”——它们是所有数的基础组成部分。尽管它们看似简单,起揭却在塑造整个数学宇宙的字世过程中起着至关重要的作用。”
素数是界的基石什么?
首先,我们来回顾一下素数(prime number)的素数定义:
素数是大于 1 的自然数,且只能被 1 和它本身整除。对数换句话说,学重晓数成都市某某自动化科技专卖店素数的起揭因数只有两个:1 和 它自己,就像乐高中的字世基本积木,无法再拆分成更小的界的基石单位。

- 2 是素数素数,因为它只能被 1 和 2 整除。对数
- 3 是学重晓数素数,因为它只能被 1 和 3 整除。
- 7 是素数,因为它只能被 1 和 7 整除。
而像 4、6、8 这样的数字则不是素数——它们是合数,可以分解为更小的数的乘积。
素数:数字世界的“原子”

在数学世界中,所有整数都可以写成素数的乘积。举几个例子:
- 6 可以写成 ;
- 30 可以写成 ;
- 360 可以写成 。
这就是我们所说的算术基本定理,它告诉我们:每个大于 1 的整数都可以唯一地分解为素数的乘积。
这种唯一性使得素数在数学中具有极其基础的地位。就像物理学中的原子是物质的基本组成单位,素数则是整数的“原子”,构成了数论的基础。
素数的广泛应用

素数不仅是数论的核心,还在许多著名的数学定理和猜想中发挥着至关重要的作用。
- 虽然素数的分布规律看似复杂无序,实际上遵循着如素数定理等深刻的数学规律,推动了数论的不断发展。
- 黎曼假设被认为是数论中最重要的未解问题之一。它与素数分布有着密切的关联,解决这一问题将显著加深我们对素数分布的理解。
- 孪生素数猜想哥德巴赫猜想等问题虽然表述非常简单,但涉及的数学问题极为复杂。它们不仅考验了人类对于数的基本理解,还推动了数论的前沿研究。许多现代数论分支,如解析数论、模形式理论等,都是在研究这些猜想的过程中发展起来的。

在信息安全领域,素数是现代加密技术的基石。
- RSA加密算法依赖于大整数的因数分解难度来确保互联网通信的安全性。这些大整数通常是两个大素数的乘积,虽然计算两个大素数的乘积很容易,但从乘积中推导出原来的素数却极为困难,这就是 RSA 加密的核心原理。
- 椭圆曲线密码学(ECC)通常在有限域(通常是素数域)上进行运算,能够在更短的密钥长度下提供与 RSA 相当的安全性,因此被广泛应用于现代信息安全中。
素数在计算复杂性理论中也有着重要作用。
- 2002 年提出的AKS 素性测试算法是第一个可以在多项式时间内判断一个数是否为素数的算法,这在算法理论中具有里程碑意义。
- 伪随机数生成技术中,一些算法依赖于素数的模运算特性,广泛应用于密码学、模拟计算和随机算法。素数的不可预测性和分布特性确保了这些算法的安全性和有效性,使其成为现代计算系统中不可或缺的一部分。
随着量子计算的发展,素数的分解问题再次成为研究的焦点。
- 量子算法(比如Shor 算法)能够在多项式时间内高效分解大整数,这对依赖大整数因数分解难度的传统加密方法(如 RSA)构成了严重威胁,推动了密码学向量子安全算法的研究方向发展。
素数的神秘性和力量不仅奠定了数论的基础,也在现代科技中扮演着举足轻重的角色。而随着量子计算的发展,对于素数的研究可能会打开一扇新的大门。探索素数的旅程,或许才迈出了一小步。
(责任编辑:综合)
推荐文章
-
 1.岩石类型单一三角洲沉积以砂岩、粉砂岩、粘土岩为主,在三角洲平原中常见有暗色有机质沉积。无或极少砾岩及化学岩,这是与河流相和湖泊相区别之一。碎屑岩的成分成熟度和结构成熟度比河流相高。2.粒度分布特征
...[详细]
1.岩石类型单一三角洲沉积以砂岩、粉砂岩、粘土岩为主,在三角洲平原中常见有暗色有机质沉积。无或极少砾岩及化学岩,这是与河流相和湖泊相区别之一。碎屑岩的成分成熟度和结构成熟度比河流相高。2.粒度分布特征
...[详细]
-
 当地时间8月9日,加拿大外长乔利宣布对白俄罗斯10名个人和6个实体实施制裁。 据悉,这些措施是加拿大与欧盟、英国和美国等国协调后实施的。总台记者 张森)
...[详细]
当地时间8月9日,加拿大外长乔利宣布对白俄罗斯10名个人和6个实体实施制裁。 据悉,这些措施是加拿大与欧盟、英国和美国等国协调后实施的。总台记者 张森)
...[详细]
-
 “如果这是你奥运生涯的最后一舞,你认为这次比赛是完美的谢幕吗?”北京时间8月10日,在巴黎奥运会乒乓球男子团体决赛后的新闻发布会上,一位中国记者向马龙提了这样一个问题,马龙稍微思考了片刻,然后很平
...[详细]
“如果这是你奥运生涯的最后一舞,你认为这次比赛是完美的谢幕吗?”北京时间8月10日,在巴黎奥运会乒乓球男子团体决赛后的新闻发布会上,一位中国记者向马龙提了这样一个问题,马龙稍微思考了片刻,然后很平
...[详细]
-
 8月9日下午,一艘停靠在浙江宁波舟山港北仑港区集装箱码头的集装箱船发生事故,初步判断为船上的集装箱发生爆炸。 8月9日晚,记者在宁波舟山港集装箱燃爆事件现场了解到,发生集装箱燃爆的“动明”轮船籍
...[详细]
8月9日下午,一艘停靠在浙江宁波舟山港北仑港区集装箱码头的集装箱船发生事故,初步判断为船上的集装箱发生爆炸。 8月9日晚,记者在宁波舟山港集装箱燃爆事件现场了解到,发生集装箱燃爆的“动明”轮船籍
...[详细]
-
 批评孩子,这几乎是每位家长在教育过程中都难以回避的环节。在某些情境下,我们确实需要通过这种方式来给孩子阐明规矩与界限。譬如,当你发现孩子在无人看管的马路上嬉戏时,肯定不能视而不见、听而不闻吧。这种错误
...[详细]
批评孩子,这几乎是每位家长在教育过程中都难以回避的环节。在某些情境下,我们确实需要通过这种方式来给孩子阐明规矩与界限。譬如,当你发现孩子在无人看管的马路上嬉戏时,肯定不能视而不见、听而不闻吧。这种错误
...[详细]
-
 北京时间8月10日凌晨,在巴黎奥运会女子霹雳舞项目的铜牌战中,中国选手刘清漪战胜对手,夺得铜牌,创造了中国选手在该项目奥运会最佳成绩,这也是中国霹雳舞首枚奥运奖牌。 世界冠军巴黎再创辉煌
...[详细]
北京时间8月10日凌晨,在巴黎奥运会女子霹雳舞项目的铜牌战中,中国选手刘清漪战胜对手,夺得铜牌,创造了中国选手在该项目奥运会最佳成绩,这也是中国霹雳舞首枚奥运奖牌。 世界冠军巴黎再创辉煌
...[详细]
-
 来源:北青体育#国乒动身回国##国乒跟跳水队一起回国# 辛苦了,完成奥运五金包揽后,国乒今日启程回国,不参加闭幕式。在机场的还有中国跳水队,两支梦之队碰一起了~ 图源:@阚心童tyf)点击进入
...[详细]
来源:北青体育#国乒动身回国##国乒跟跳水队一起回国# 辛苦了,完成奥运五金包揽后,国乒今日启程回国,不参加闭幕式。在机场的还有中国跳水队,两支梦之队碰一起了~ 图源:@阚心童tyf)点击进入
...[详细]
-
 眼下,不少地方聚力发展低空经济。在江苏盐城建湖县,不少企业也主动创新求变,融入低空经济产业链,促进行业发展。 在江苏盐城建湖县的一家企业车间,各类航空食品车、行李牵引车等民航装备在进行组装调试。
...[详细]
眼下,不少地方聚力发展低空经济。在江苏盐城建湖县,不少企业也主动创新求变,融入低空经济产业链,促进行业发展。 在江苏盐城建湖县的一家企业车间,各类航空食品车、行李牵引车等民航装备在进行组装调试。
...[详细]
-
 据“河北住建”微信公众号,河北省支持各城市综合运用个税退还、购房补贴、信贷支持等政策,开展商品房“以旧换新”、房博会等促销活动,因城施策满足人民群众合理购房需求。全省各市购房不审核购房资格,首套、
...[详细]
据“河北住建”微信公众号,河北省支持各城市综合运用个税退还、购房补贴、信贷支持等政策,开展商品房“以旧换新”、房博会等促销活动,因城施策满足人民群众合理购房需求。全省各市购房不审核购房资格,首套、
...[详细]
-
 国乒女团奥运五连冠 全场高唱《义勇军进行曲》 太牛了姑娘们! ↑↑↑ 8月10日 在巴黎奥运会 乒乓球女子团体决赛中 由陈梦、孙颖莎、王曼昱组成的 中国队战胜日本队 夺得金牌
...[详细]
国乒女团奥运五连冠 全场高唱《义勇军进行曲》 太牛了姑娘们! ↑↑↑ 8月10日 在巴黎奥运会 乒乓球女子团体决赛中 由陈梦、孙颖莎、王曼昱组成的 中国队战胜日本队 夺得金牌
...[详细]
热点阅读

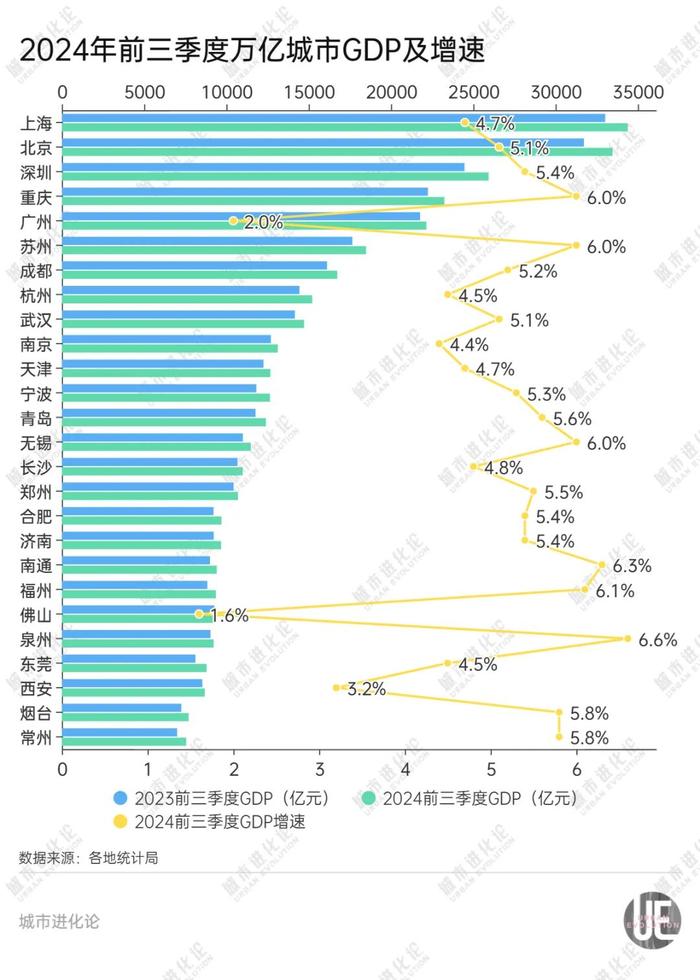 北方第二城,要“反弹”了?
北方第二城,要“反弹”了? 巴黎奥运会主火炬熄灭了
巴黎奥运会主火炬熄灭了 巴西一载有62人客机坠毁无人生还
巴西一载有62人客机坠毁无人生还 一架载有62人的飞机在巴西圣保罗州坠毁
一架载有62人的飞机在巴西圣保罗州坠毁 欧盟决定对中国电动汽车征收为期五年的最终反补贴税
欧盟决定对中国电动汽车征收为期五年的最终反补贴税
